Understanding Matrices: Solving Complex Problems in the Real World

Introduction to Matrices

Matrices are rectangular arrays of numbers, symbols, or expressions, arranged in rows and columns. They are fundamental tools in mathematics, providing a concise way to represent and manipulate data. The historical development of matrices dates back to ancient civilizations, but they gained prominence in the 19th century with the work of mathematicians like Arthur Cayley and James Sylvester.

Matrices are essential in various fields, including physics, engineering, computer science, and economics, due to their ability to simplify complex calculations and represent multi-dimensional data.

Understanding Matrix Operations

Addition and Subtraction

Matrix addition and subtraction involve combining two matrices of the same dimensions by adding or subtracting their corresponding elements. For example:

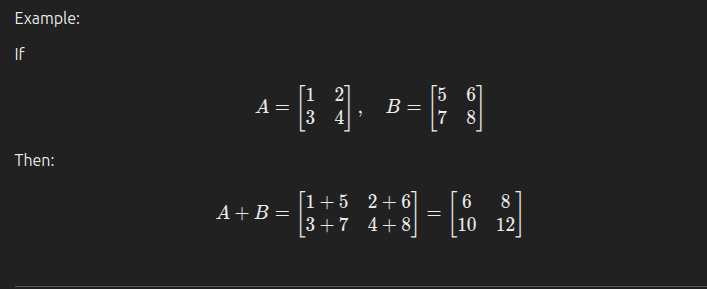
Matrix Multiplication

Matrix multiplication is more complex and involves the dot product of rows and columns. For two matrices A (of size m × n) and B (of size n × p), the resulting matrix C (of size m × p) is computed as follows:

Determinants and Inverse Matrices

The determinant of a square matrix is a scalar value that helps determine whether the matrix is invertible.

The inverse of a matrix A, denoted as A⁻¹, satisfies the equation: where I is the identity matrix.

Real-World Applications

Computer Graphics and 3D Transformations

Matrices are crucial in computer graphics for transforming shapes and images. They enable operations like rotation, scaling, and translation of 3D objects.

Machine Learning and Neural Networks

In machine learning, matrices are used to represent datasets and perform operations in neural networks, such as weight adjustments during training.

Digital Image Processing

Images can be represented as matrices, where each element corresponds to a pixel's intensity. Matrix operations facilitate filtering, transformations, and enhancements.

Economics and Finance (Input-Output Models)

Matrices are employed in economics to model the relationships between different sectors, helping to analyze the flow of goods and services.

Quantum Mechanics

In quantum mechanics, state vectors and operators are represented as matrices, allowing for the mathematical formulation of physical phenomena.

Search Engines and PageRank Algorithm

Google’s PageRank algorithm uses matrices to rank web pages based on their link structures, analyzing the connectivity of the web.

Engineering (Structural Analysis)

Matrices are utilized in engineering to analyze forces and stresses in structures, aiding in the design and safety assessments.

Problem-Solving with Matrices

Linear Systems of Equations

Matrices provide a systematic way to solve linear equations using techniques like Gaussian elimination or matrix inversion.

Network Analysis

In network theory, matrices represent connections and flows, enabling the analysis of social networks, transportation systems, and more.

Optimization Problems

Matrices are integral in optimization problems, particularly in linear programming, where they help define constraints and objectives.

Data Compression

Matrix transformations, such as Singular Value Decomposition (SVD), are used in data compression techniques, reducing storage requirements while preserving essential information.

Error Correction Codes

Matrices play a vital role in coding theory, particularly in designing error correction codes that ensure data integrity during transmission.

Matrices in Modern Technology

Computer Vision

Matrices are at the core of computer vision algorithms, enabling machines to interpret and analyze visual data.

Facial Recognition

Facial recognition systems use matrices to process and compare facial features, enhancing security and user identification.

Recommendation Systems

Matrix factorization techniques are employed in recommendation systems, such as those used by Netflix and Amazon, to suggest content based on user preferences.

Game Development

In game development, matrices are used for physics simulations, rendering graphics, and managing object transformations.

Scientific Simulations

Matrices enable scientists to model complex systems and simulate real-world phenomena, from climate models to molecular dynamics.

Benefits and Advantages

Efficient Data Organization

Matrices allow for structured data representation, making it easier to manipulate and analyze large datasets.

Parallel Processing

Matrix operations can be parallelized, significantly speeding up computations in high-performance computing environments.

Complex Calculations Simplification

Matrices simplify complex calculations, allowing for more efficient problem-solving in various applications.

Pattern Recognition

Matrices facilitate pattern recognition in data analysis, enabling the identification of trends and anomalies.

System Modeling

Matrices provide a framework for modeling real-world systems mathematically, aiding in predictions and analyses.

Future Perspectives

Emerging Applications

As technology evolves, matrices are finding new applications in fields like bioinformatics, robotics, and smart cities.

Role in Quantum Computing

Matrices are essential in quantum computing, providing the mathematical foundation for quantum algorithms and operations.

Advanced AI Applications

With the rise of advanced AI, matrices will play a critical role in developing more sophisticated models and algorithms.

New Mathematical Developments

Research in matrix theory continues to advance, leading to new techniques and applications in various scientific disciplines.

Practical Examples and Case Studies

Google's PageRank Implementation

Google's PageRank algorithm uses matrices to analyze the web's link structure, ranking pages based on their importance and relevance.

Netflix Recommendation System

Netflix employs matrix factorization to analyze user preferences and suggest content tailored to individual tastes.

Computer Animation in Pixar Movies

Pixar uses matrices to perform complex transformations and animations, bringing characters and scenes to life.

Engineering Structure Analysis

Engineers use matrices to analyze and design structures, ensuring safety and stability in buildings and bridges.

Conclusion

Matrices are powerful mathematical tools that help solve complex problems across various fields. Their applications in technology, science, and everyday life demonstrate their significance in modern society. As we continue to explore new frontiers, the role of matrices will only grow, paving the way for innovative solutions and advancements.